全连接神经网络

全连接神经网络简介

对于全连接神经网络，相信很多读者一听到“网络”二字，头皮就开始发麻，笔者一开始学的时候也一样，觉得网络密密麻麻地，绝对很难，其实不然，这里的网络比我们现实生活中的网络简化了不止一丁点儿，但是它却能出奇地完成各种各样的任务，逐渐成为我们人类智能生活的璀璨明珠。当然，虽然全连接神经网络并不是最耀眼的一颗，但却是每一个初学的读者必须去了解的一颗，在这里，笔者认为全连接神经网络是每位读者深度学习之旅的开端。

全连接神经网络原理

光看名字，可能大家并不了解这个网络是干啥的，那么笔者先给大家附上一张图，如下图所示。它作为神经网络家族中最简单的一种网络，相信大家看完它的结构之后一定会对它有个非常直观的了解。

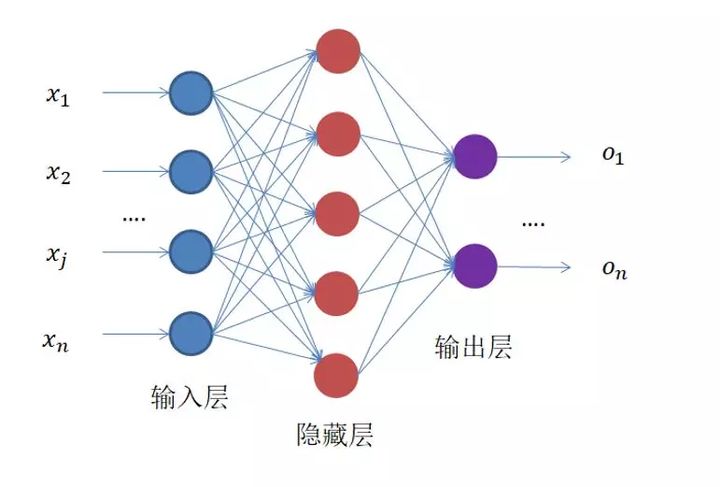
对，就是这么一个东西，左边输入，中间计算，右边输出。可能这样还不够简单，笔者给大家画一个更简单的运算示意图，如下图所示。

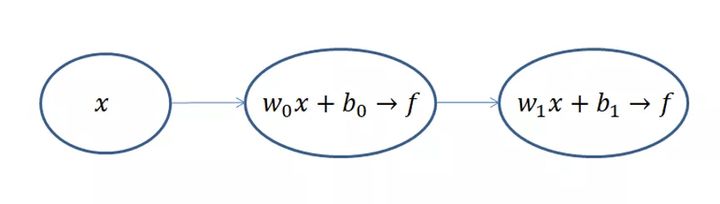
不算输入层，上面的网络结构总共有两层，隐藏层和输出层，它们“圆圈”里的计算都是公式(1)和(2)的计算组合：

$$a = wx +b$$ $$f(z) = \frac {1} {e^{-z}}$$

每一级都是利用前一级的输出做输入，再经过圆圈内的组合计算，输出到下一级。

看到这里，可能很多人会疑惑，为什么要加上f(z)这个运算，这个运算的目的是为了将输出的值域压缩到（0,1），也就是所谓的归一化，因为每一级输出的值都将作为下一级的输入，只有将输入归一化了，才会避免某个输入无穷大，导致其他输入无效，变成“一家之言”，最终网络训练效果非常不好。

此时，有些记忆力比较好的读者可能会想，反向传播网络？反向去哪了？对的，这个图还没画完整，整个网络结果结构应该是这样，如下图所示。

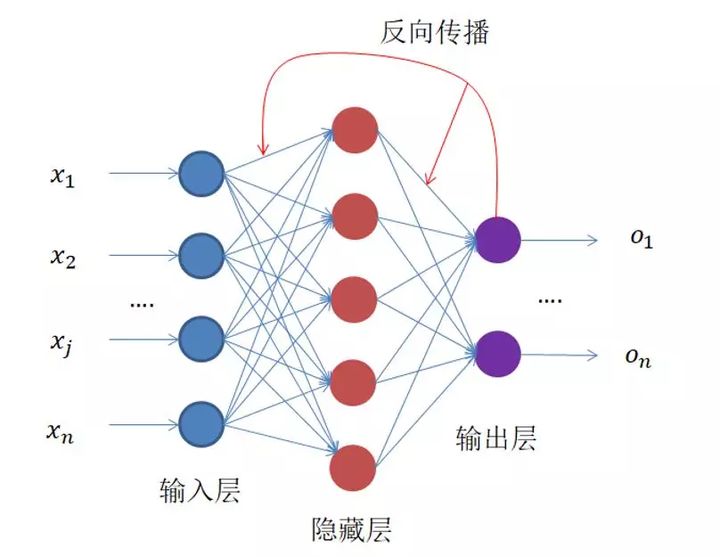
那有些读者又会提出新的问题了，那反向传播的东西到底是什么呢？目的又是什么呢？这里，所有读者都要有这么一点认识，神经网络的训练是有监督的学习，也就是输入X 有着与之对应的真实值Y ，神经网络的输出Y 与真实值Y 之间的损失Loss 就是网络反向传播的东西。整个网络的训练过程就是不断缩小损失Loss 的过程。为此，就像高中一样，我们为了求解某个问题，列出了一个方程，如公式(3)~(5)：

$$Loss = \sum_{i=1}^{n} (y_i - (wx_i + b))^2$$ $$Loss=\sum_{i=1}^n(x_i^2w^2 + b^2 + 2x_iwb+ 2y_ib - 2x_iy_iw + y_i ^2)$$ $$Loss = \sum_{i=1}^n{Aw^2 + Bb^2 +Cwb - Db-Ew+F}$$

上述的公式经过化简，我们可以看到A、B、C、D、E、F都是常系数，未知数就是w 和b ，也就是为了让Loss 最小，我们要求解出最佳的w 和b 。这时我们稍微想象一下，如果这是个二维空间，那么我们相当于要找一条曲线，让它与坐标轴上所有样本点距离最小。比如这样，如下图所示。

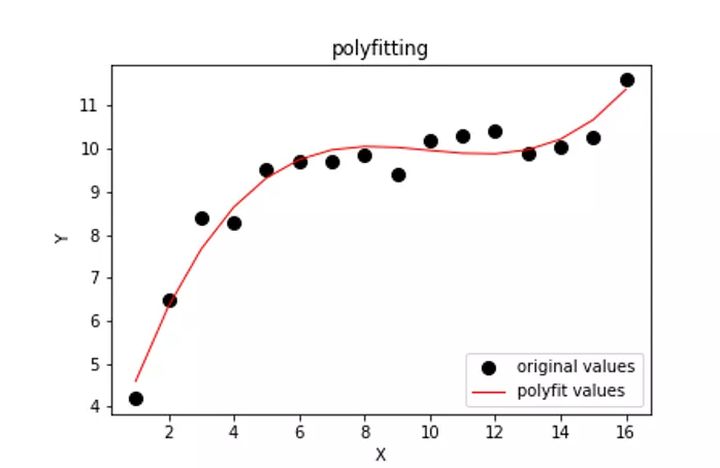
同理，我们可以将Loss方程转化为一个三维图像求最优解的过程。三维图像就像一个“碗”，如下图所示，它和二维空间的抛物线一样，存在极值，那我们只要将极值求出，那就保证了我们能求出最优的（w , b）也就是这个“碗底”的坐标，使Loss 最小。

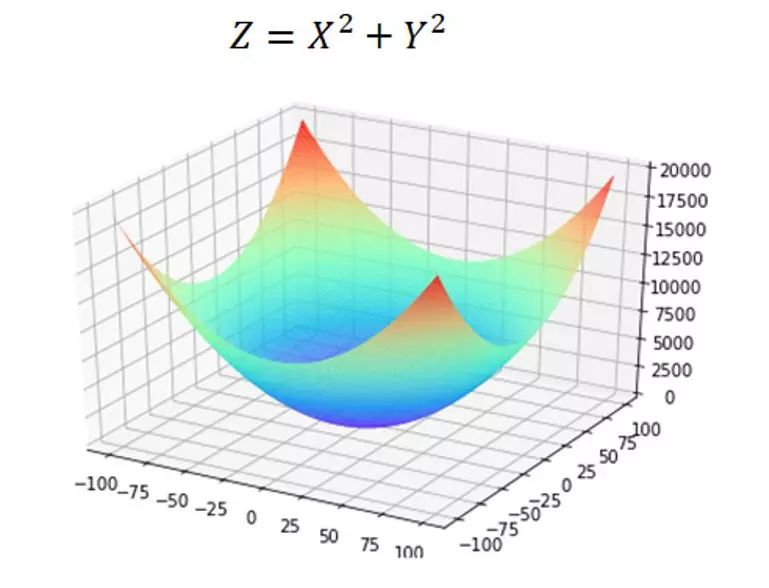
那说了这么多，我们应该如何求解呢？

读者们是否还记得上高中的时候，当我们列完函数方程之后，做的第一件事就是对这个函数求导，是的，这里也一样，要求极值，首先求导。不过，我们高中没有接触过二元凸函数的求导，但是相信翻阅此书的读者应该都是大学生，这时候要拿出高等数学这本书来了，偏导数在这里隆重登了场。偏导数简单来讲，也就是对X，Y分别求导，在求导过程中，把其他的未知量当成常数即可。

好了，理论知识补充完了，这时候我们想象自己在一座山上，要想从山上最快地去到谷底，那就要沿着最陡峭的地方往下走。这个最陡峭的地方，我们叫做梯度，像不像我们对上面那个“碗”做切线，找出最陡的那条切线，事实上我们做的就是这个，求偏导就是这么一个过程。

$$梯度 \nabla =\begin{pmatrix} \frac {\partial f(x, y)} {\partial x}, \frac {\partial f(x, y)} {\partial y}\end{pmatrix}$$

我们每走一步，坐标就会更新：

$$x_{n+1} = x_n - \alpha * \frac {\partial f(x, y)} {\partial {x}}$$ $$y_{n+1} = y_n - \alpha * \frac {\partial f(x, y)} {\partial {y}}$$

当然，这是三维空间中的，假如我们在多维空间漫步呢，其实也是一样的，也就是对各个维度求偏导，更新自己的坐标。

$$\nabla = \begin{pmatrix} \frac {\partial f(x, y)} {\partial w_1}, \frac {\partial f(x, y)} {\partial w_2}, \frac {\partial f(x, y)} {\partial w_3}, ···， \frac {\partial f(x, y)} {\partial w_n} \end{pmatrix}$$ $$w_{i+1} = w - \alpha * \frac {\partial f(x, y)} {\partial w^i}$$

其中，w的上标i表示第几个w，下标n表示第几步，α是学习率，后面会介绍α的作用。所以，我们可以将整个求解过程看做下山（求偏导过程），为此，我们先初始化自己的初始位置。

$$(w_0, y_0)$$ $$w_1 = w_0 - \alpha * \frac {\partial Loss(w,b)} {\partial w}$$ $$b_1 = b_0 - \alpha * \frac {\partial Loss(w,b)} {\partial b}$$

这样我们不断地往下走（迭代），当我们逐渐接近山底的时候，每次更新的步伐也就越来越小，损失值也就越来越小，直到达到某个阈值或迭代次数时，停止训练，这样找到 就是我们要求的解。

我们将整个求解过程称为梯度下降求解法。

这里还需要补充的是为什么要有学习率α，以及如何选择学习率α？

通常来说，学习率是可以随意设置，你可以根据过去的经验或书本资料选择一个最佳值，或凭直觉估计一个合适值，一般在（0，1）之间。这样做可行，但并非永远可行。事实上选择学习率是一件比较困难的事，图 4.7显示了应用不同学习率后出现的各类情况，其中epoch为使用训练集全部样本训练一次的单位，loss表示损失。

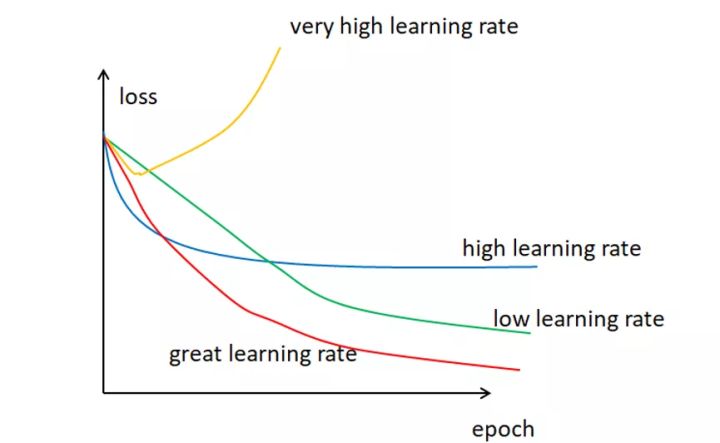
可以发现，学习率直接影响我们的模型能够以多快的速度收敛到局部最小值（也就是达到最好的精度）。一般来说，学习率越大，神经网络学习速度越快。如果学习率太小，网络很可能会陷入局部最优；但是如果太大，超过了极值，损失就会停止下降，在某一位置反复震荡。

也就是说，如果我们选择了一个合适的学习率，我们不仅可以在更短的时间内训练好模型，还可以节省各种运算资源的花费。

如何选择？业界并没有特别硬性的定论，总的来说就是试出来的，看哪个学习率能让Loss收敛得更快，Loss最小，就选哪个。

全连接神经网络小结

可能很多读者在看到第4.1节内容的时候会认为，既然深度学习已经将整个梯度下降的求解过程都封装好了，笔者为什么还要花这么大的篇幅来讲解呢？

因为我们后续接触的CNN，RNN等神经网络的原理和训练过程都是差不多的，无非就是网络结构改变罢了，在这里把最基本的原理掌握了，后面就算碰到再复杂的网络结构也不会慌张。

另外，当大家专研理论至深处且需要设计一个新的网络结构时，那时我们对原理掌握的熟练程度直接决定着所设计网络结构的优劣。

参考资料

深度学习开端｜全连接神经网络